Masking
You know I can't hear you when the water is running!
This statement carries the essentials of the conventional wisdom about sound masking. Low-frequency, broad banded sounds (like water running) will mask higher frequency sounds which are softer at the listener's ear (a conversational tone from across the room). For a single frequency masking tone, masking curves can be determined experimentally. Also, from the idea of the just noticeable difference in sound intensity, one can approximately calculate the amount of a added second sound that would exceed the jnd and thus be audible.
Broadband white noise tends to mask all frequencies, and is approximately linear in that masking. By linear you mean that if you raise the white noise by 10 dB, you have to raise everything else 10 dB to hear it.
|
Index
Loudness concepts
Hearing concepts |

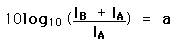
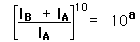
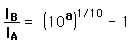
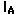 in dB to get the threshold for
in dB to get the threshold for 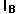 which could just be heard.
which could just be heard.