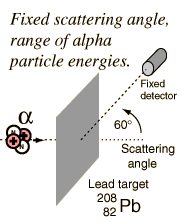
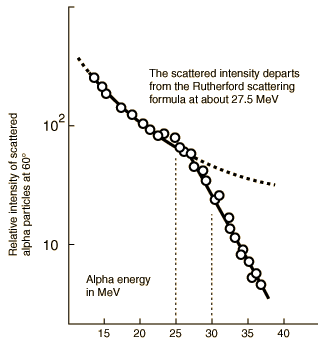
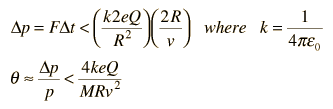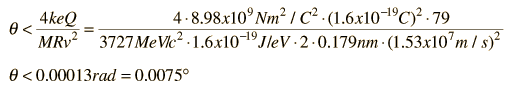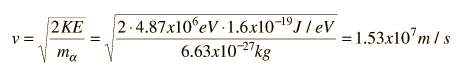Evidence for Nuclear Interaction

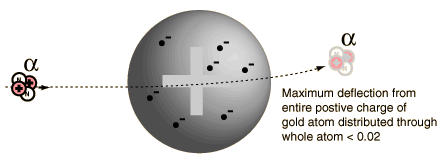
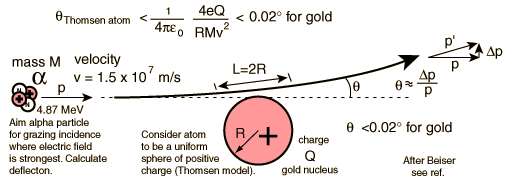
Rutherford and colleagues were able to calculate the number of alpha particles which would be scattered into any angle based upon the number of nuclei and their spacing in the gold foil. The observations agreed with these calculations up to a certain large angle where they got significant deviations. This indicated a new interaction force and was interpreted as "hitting" the nucleus. This scattering angle could be used to calculate the distance of closest approach and therefore the "radius" of the nucleus.

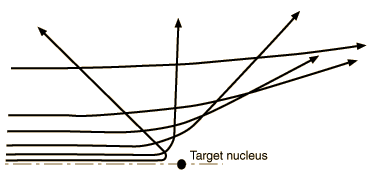The distance from the path of the alpha particle to the centerline is called the impact parameter. The smaller the impact parameter, the larger the angle of deflection.

The Thomson Model of the Atom

At the turn of the century, the prevalent view of the atom was a positively charged blob with sprinkled negatively charged electrons in it, a "raisin pudding" model of the atom.

The conservation of momentum and energy for an elastic collision dictate that the angle must be less than 90 degrees if the projectile is more massive than the target. But in the Rutherford scattering experiment, Geiger and Marsden showed that 1 in 8000 alpha particles scattered with angle >90 degrees.

Alpha Scattering by Charge Cloud

The Rutherford scattering experiment put to rest the Thomson model of the atom, because it could be shown that a positive charge distributed throughout the classical volume of the atom could not deflect the alpha particles by more than a small fraction of a degree.

The calculation of an upper bound on the change in momentum Dp for the alpha particle can be approached in terms of the impulse of force relationship FDt = Dp. Making use of the Coulomb force expression:

For the specific case of the 4.87 MeV alpha particle from radium-226, this estimate of the angle becomes

This calculation uses the radius 0.179 nm for the gold atom from the periodic table. It also includes the following velocity for the alpha particle calculated from the non-relativistic kinetic energy expression.

The insight gained by Rutherford and his research team, including Geiger and Marsden, was that the current picture of the atomic volume as being filled with positively charged matter could not be correct since they saw alpha deflections of more than 90°. It also told them that with radii much smaller than the atom, they could get large deflections. So this table-top experiment gave birth to the picture of the atomic nucleus as a small central core of positively charged matter, and the reasoning followed from strictly classical physics.

Departure From Rutherford Formula

Scattering of high energy alpha particles at a fixed angle can be used to estimate nuclear radius.

Eisberg, R. M. and Porter, C. E., Rev. Mod. Phys. 33, 190 (1961)

The mutual Coulomb repulsion of an alpha particle and a target nucleus give rise to a predictable trajectory and led to the development of the Rutherford formula. As the Geiger-Marsden data shows, the data are in agreement with the formula for a wide range of angles. With high enough alpha energies, however, the projectile punches in close enough to the nuclear center to come into range of the nuclear strong force and the distribution of scattered alphas departs from the Rutherford formula.

Considering the data above for scattering from ²⁰⁸Pb, you can use the point of departure from the Rutherford scattering formula to estimate the nuclear radius. From the closest approach calculation for this energy and angle, the impact parameter is 7.44 fm and the closest approach is 12.9 fm. If you use the nuclear radius calculation, you get 7.1 fm as the radius of this nucleus. So the estimate is not precise, but is certainly in the right range for the nucleus. It was enlightening in an era when many people thought the Thomson model applied to the positive charge in the atom - an error of about 4 orders of magnitude! But the best data for those radii were obtained from electron scattering.