Alpha Halflife vs Kinetic Energy
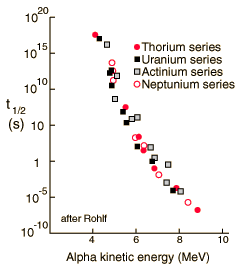 |
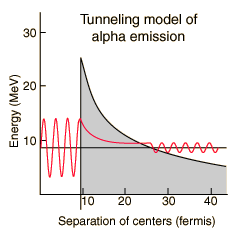
The half-lives of heavy elements which emit alpha particles varies over 20 orders of magnitude, from about a tenth of a microsecond to 10 billion years. This half-life range depends strongly on the observed alpha kinetic energy which varies only about a factor of two; from about 4 to 9 MeV. This extraordinary dependence upon kinetic energy suggests an exponential process, and is modeled by quantum mechanical tunneling through the Coulomb barrier. |
References
Rohlf
Sec 7-4
Eisberg & Resnick
Sec 16-2
| HyperPhysics***** Nuclear | R Nave |