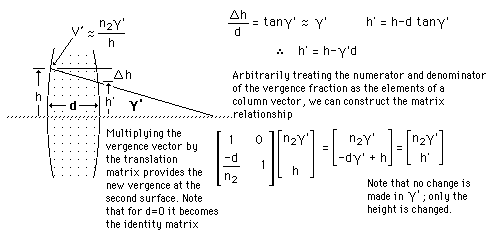
System Matrix
For systems of multiple thick lenses, it is sometimes useful to represent the system by a system matrix. The matrix is built up by multiplying the refraction matrices and translation matrices. The positions of the principal planes, the front and back surface powers, and the equivalent focal length of Gullstrand's equation can be calculated from the system matrix.
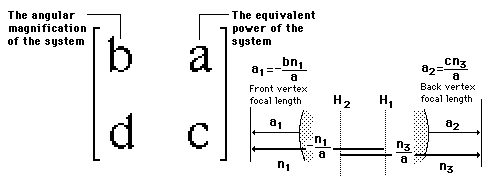
This is the form of the system matrix used by Meyer-Arendt. An alternate form is used by Hecht.
| Calculations | Alternate form of system matrix: Hecht form |
Lens concepts
Thick lens concepts
References
Meyer-Arendt
Hecht
| HyperPhysics***** Light and Vision | R Nave |