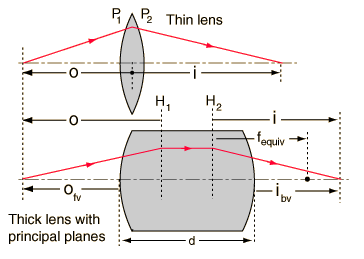
Principal Planes
The principal planes are two hypothetical planes in a lens system at which all the refraction can be considered to happen. For a given set of lenses and separations, the principal planes are fixed and do not depend upon the object position. The thin lens equation can be used, but it leaves out the distance between the principal planes. The focal length f is that given by Gullstrand's equation. The principal planes for a thick lens are illustrated. For practical use, it is often useful to use the front and back vertex powers.
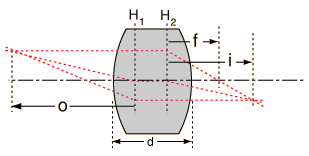
| Calculation for single lens | Image distance from principal planes |
Lens concepts
Thick lens concepts
| HyperPhysics***** Light and Vision | R Nave |