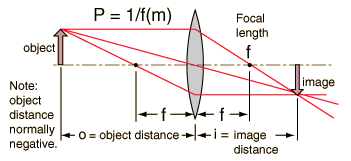
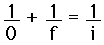Thin Lens Equation

A common Gaussian form of the lens equation is shown below. This is the form used in most introductory textbooks. A form using the Cartesian sign convention is often used in more advanced texts because of advantages with multiple-lens systems and more complex optical instruments. Either form can be used with positive or negative lenses and predicts the formation of both real and virtual images. Does not apply to thick lenses.

For a lens of focal length f = cm, corresponding to lens power P = diopters, an object distance of o = cm will produce an image at i = cm. The linear magnification will be M = .

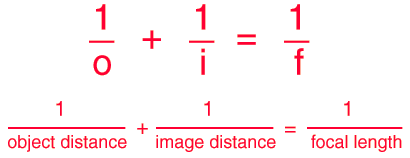
If the lens equation yields a negative image distance, then the image is a virtual image on the same side of the lens as the object. If it yields a negative focal length, then the lens is a diverging lens rather than the converging lens in the illustration. The lens equation can be used to calculate the image distance for either real or virtual images and for either positive on negative lenses. The linear magnification relationship allows you to predict the size of the image.

Thin-Lens Equation:Cartesian Convention

The thin-lens equation in the Gaussian form is

where the Cartesian sign convention has been used. The lens equation is also sometimes expressed in the Newtonian form. The derivation of the Gaussian form proceeds from triangle geometry. For a thin lens, the lens power P is the sum of the surface powers. For thicker lenses, Gullstrand's equation can be used to get the equivalent power.

Cartesian Sign Convention

1. All figures are drawn with light traveling from left to right.
2. All distances are measured from a reference surface, such as a wavefont or a refracting surface. Distances to the left of the surface are negative.
3. The refractive power of a surface that makes light rays more convergent is positive. The focal length of such a surface is positive.
4. The distance of a real object is negative.
5. The distance of a real image is positive.
6. Heights above the optic axis are positive.
7. Angles measured clockwise from the optic axis are negative.

Because the direction of light travel is consistent and there is a consistent convention to determine the sign of all distances in a calculation, this sign convention is used in many texts. It has some advantages when dealing with multilens systems and more complex optical instruments.