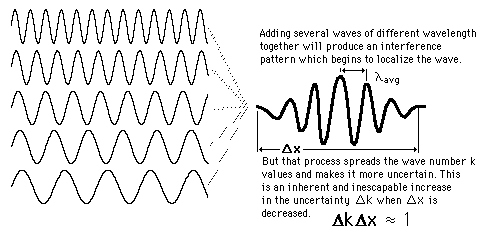
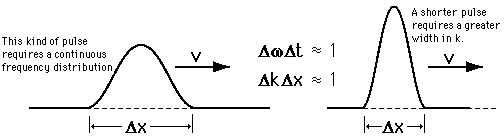Wave Packet Solution
Since the traveling wave solution to the wave equation
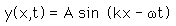
is valid for any values of the wave parameters, and since any superposition of solutions is also a solution, then one can construct a wave packet solution as a sum of traveling waves:
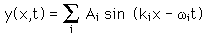
For a continuous range of wave vectors k, the sum is replaced by an integral:
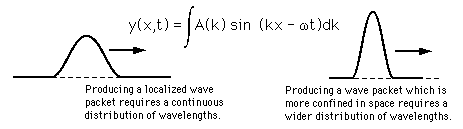
| Wave packet details |
Wave concepts
Reference
Tipler
Elementary Modern Physics, Appendix B