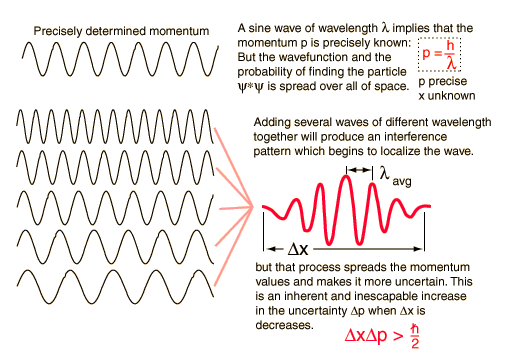
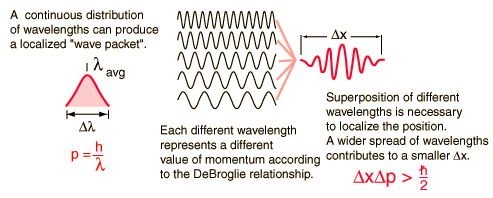
The Uncertainty Principle

The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. There is a minimum for the product of the uncertainties of these two measurements. There is likewise a minimum for the product of the uncertainties of the energy and time.

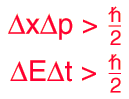
This is not a statement about the inaccuracy of measurement instruments, nor a reflection on the quality of experimental methods; it arises from the wave properties inherent in the quantum mechanical description of nature. Even with perfect instruments and technique, the uncertainty is inherent in the nature of things.

Uncertainty Principle

Important steps on the way to understanding the uncertainty principle are wave-particle duality and the DeBroglie hypothesis. As you proceed downward in size to atomic dimensions, it is no longer valid to consider a particle like a hard sphere, because the smaller the dimension, the more wave-like it becomes. It no longer makes sense to say that you have precisely determined both the position and momentum of such a particle.

Particle Confinement

Confinement Calculation