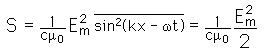Electromagnetic Wave Equation
The wave equation for a plane electric wave is
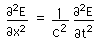
with the same form applying to the magnetic field wave in a plane perpendicular the electric field. The wave equation for electromagnetic waves arises from Maxwell's equations. The form of a plane wave solution for the electric field is
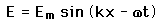
and that for the magnetic field
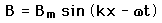
To be consistent with Maxwell's equations, these solutions must be related by
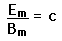
| Transport of energy by electromagnetic waves |
Wave concepts
Electromagnetic wave concepts
Electromagnetic spectrum
| HyperPhysics*****Electricity and Magnetism | R Nave |
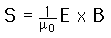
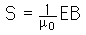
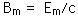 so that the average intensity for a plane wave can be written
so that the average intensity for a plane wave can be written