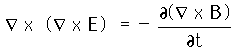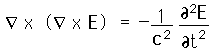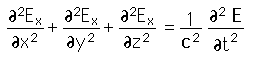Charge Conservation
The fundamental idea of charge conservation is contained in Maxwell's Equations. If we take the divergence of the differential form of Ampere's law:
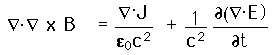
The first term above is zero by identity, and using Gauss' law:

the result is:
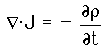
The implication here is that the current through any enclosed surface is equal to the time rate of charge within the surface. This is an important test of Maxwell's equations since all experimental evidence points to charge conservation.
| Maxwell's Equations |
Maxwell's equations concepts