Driven Oscillator Examples
If a damped oscillator is driven by an external force, the solution to the motion equation has two parts, a transient and a steady-state part, which must be used together to fit the physical boundary conditions of the problem.
|
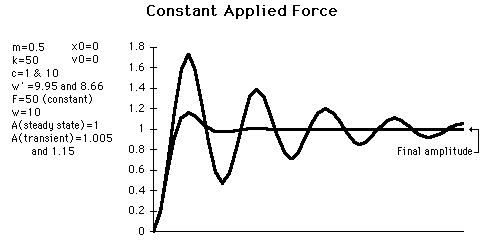
If a constant force is applied to a damped oscillator, it will stretch out to a final position determined by its spring constant. However, depending upon the initial conditions, it may oscillate about that final position and then settle down to the final position. This is the practical implication of the transient solution to the motion equations.
| |
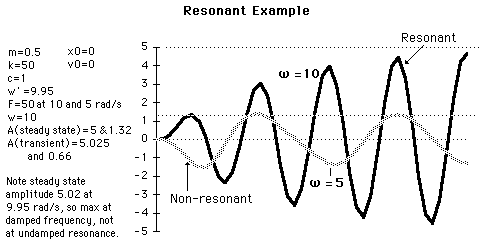
If a sinusoidal driving force is applied at the resonant frequency of the oscillator, then its motion will build up in amplitude to the point where it is limited by the damping forces on the system. If the damping forces are small, a resonant system can build up to amplitudes large enough to be destructive to the system. Such was the famous case of the Tacoma Narrows Bridge, which was blown down by the wind when it responded to a component in the wind force which excited one of its resonant frequencies.
| |
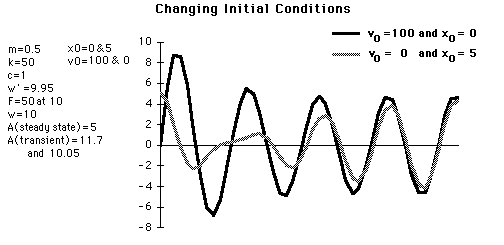
The effect of the transient solution on the behavior of a damped oscillator is strongly dependent upon the initial conditions. Although a driven system will ultimately settle down to a behavior determined by the driving force (steady-state solution), the early part of the motion can show a lot of variety.
| |
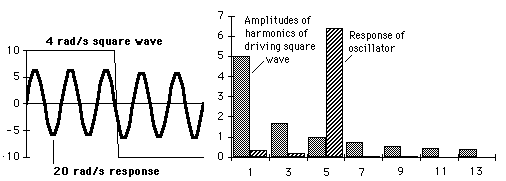
It is the nature of a resonant system to respond strongly to influences which have frequencies close to its resonant frequency. If a complex exciting force is applied, i.e., one which will have many frequency components, then the system will tend to pick out the components which are close to its resonant frequency. The example given is that of a square-wave driving force |
|
Index
Periodic motion concepts
Driven oscillator |