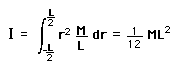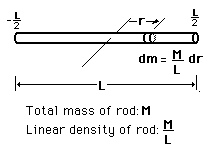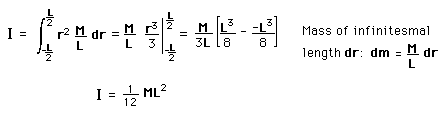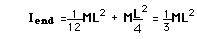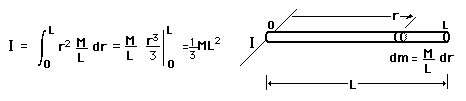Rotational and Linear Example

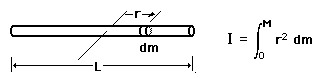
A mass m is placed on a rod of length r and negligible mass, and constrained to rotate about a fixed axis. If the mass is released from a horizontal orientation, it can be described either in terms of force and accleration with Newton's second law for linear motion, or as a pure rotation about the axis with Newton's second law for rotation. This provides a setting for comparing linear and rotational quantities for the same system. This process leads to the expression for the moment of inertia of a point mass.

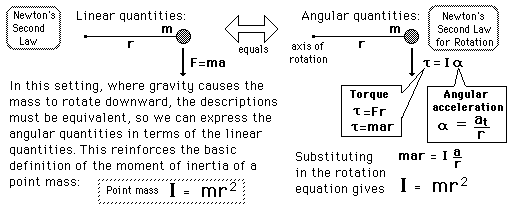
Moment of Inertia: Rod

For a uniform rod with negligible thickness, the moment of inertia about its center of mass is

For mass M = kg and length L = m, the moment of inertia is I = kg m² Show

The moment of inertia about the end of the rod can be calculated directly or obtained from the center of mass expression by use of the Parallel axis theorem.

The moment of inertia about the end of the rod is I = kg m². Show

If the thickness is not negligible, then the expression for I of a cylinder about its end can be used.

Moment of Inertia: Rod

Calculating the moment of inertia of a rod about its center of mass is a good example of the need for calculus to deal with the properties of continuous mass distributions. The moment of inertia of a point mass is given by I = mr^2 , but the rod would have to be considered to be an infinite number of point masses, and each must be multiplied by the square of its distance from the axis. The resulting infinite sum is called an integral. The general form for the moment of inertia is:

When the mass element dm is expressed in terms of a length element dr along the rod and the sum taken over the entire length, the integral takes the form:

Show details

Rod Moment Calculation

The moment of inertia calculation for a uniform rod involves expressing any mass element in terms of a distance element dr along the rod. Since the total length L has mass M, then M/L is the proportion of mass to length and the mass element can be expressed as shown. Integrating from -L/2 to +L/2 from the center includes the entire rod. The integral is of polynomial type:

Rod Moment About End

Once the moment of inertia of an object about its center of mass has been determined, the moment about any other axis can be determined by the Parallel axis theorem:

In this case that becomes

This can be confirmed by direct integration