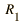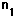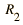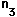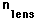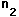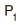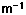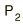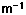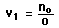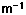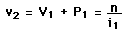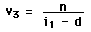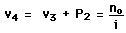Thick Lens in Different Media
This page is under construction - the Javascript calculation will be added.
Tracing the vergence is a convenient way to locate the image formed by a thick lens in media of different indices of refraction. The Cartesian sign convention is used.
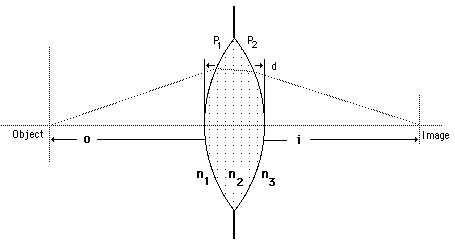A thick lens can be characterized by its radii of curvature, its index of refraction, and its thickness.
| Radius | 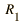 | = m, index |  | = |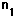
| Radius | 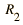 | = m, index |  | = |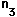
| Index |  | = |  | = |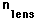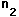
Note that for the geometry illustrated, R1 is a positive number and R2 is negative since it points back in the direction from which the light came.
The vergences can be calculated from the lens parameters and the object distance.The change in vergence when the light encounters a refracting surface is equal to the power of the surface:
Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel.
The surface powers of the lens are determined by the radii of curvature.
 | = |  |
 | = | |
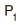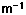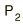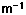The vergences can then be calculated.
 | = | |
 | = | |
 | = | |
 | = | |
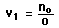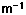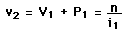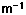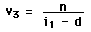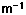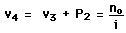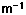The exit vergence from the final surface determines the image distance with respect to that surface.
This can be compared with the image distance for a thin lens with the same surface powers:
| Image distance i(thin) = m |
The power of a thin lens is just the sum of the surface powers:
 | = | |
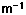The equivalent power for the thick lens can be calculated from Gullstrand's equation:
 | = | |
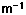Note that the calculation does not take into account the change in lens thickness with the angle of the incoming ray. It is typical to do the calculation only for the paraxial rays where the departure from full thickness is negligible.
|