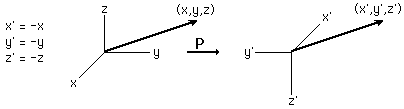Parity

Parity involves a transformation that changes the algebraic sign of the coordinate system. Parity is an important idea in quantum mechanics because the wavefunctions which represent particles can behave in different ways upon transformation of the coordinate system which describes them. Under the parity transformation:

The parity transformation changes a right-handed coordinate system into a left-handed one or vice versa. Two applications of the parity transformation restores the coordinate system to its original state.

It is a reasonable presupposition that nature should not care whether its coordinate system is right-handed or left-handed, but surprisingly, that turns out not to be so. In a famous experiment by C. S. Wu, the non-conservation of parity in beta decay was demonstrated.

Non-conservation of Parity

The electromagnetic and strong interactions are invariant under the parity transformation. It was a reasonable assumption that this was just the way nature behaved, oblivious to whether the coordinate system was right-handed or left-handed. But for several years physicists had puzzled over the decay of the neutral kaons, which had equal mass but decayed to products of opposite parity. In 1956, T. D. Lee and C. N. Yang predicted the nonconservation of parity in the weak interaction. Their prediction was quickly tested when C. S. Wu and collaborators studied the beta decay of Cobalt-60 in 1957. By lowering the temperature of cobalt atoms to about 0.01K, Wu was able to "polarize" the nuclear spins along the direction of an applied magnetic field. The directions of the emitted electrons were then measured. Equal numbers of electrons should be emitted parallel and antiparallel to the magnetic field if parity is conserved, but they found that more electrons were emitted in the direction opposite to the magnetic field and therefore opposite to the nuclear spin.

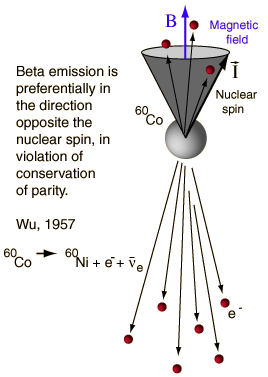This and subsequent experiments have consistently shown that a neutrino always has its intrinsic angular momentum (spin) pointed in the direction opposite its velocity. It is called a left-handed particle as a result. Anti-neutrinos have their spins parallel to their velocity and are therefore right-handed particles. Therefore we say that the neutrino has an intrinsic parity.

The idea that nature at a very fundamental level can tell the difference between "left-handed" and "right-handed" systems is a radical one. It was thought for a time that the combination of the parity operation (=P) and "charge conjugation" (changing each particle into its antiparticle = C) was an inviolate conservation law (CP invariance). But the study of the Kaon decay in 1964 showed a violation of CP. If you add time reversal (=T) to the picture, then it appears that the combination of all three leaves the system indistinguishable from the original (CPT invariance).