The Fermi-Dirac Distribution
The Fermi-Dirac distribution applies to fermions, particles with half-integer spin which must obey the Pauli exclusion principle. Each type of distribution function has a normalization term multiplying the exponential in the denominator which may be temperature dependent. For the Fermi-Dirac case, that term is usually written:

The significance of the Fermi energy is most clearly seem by setting T=0. At absolute zero, the probability is =1 for energies less than the Fermi energy and zero for energies greater than the Fermi energy. We picture all the levels up to the Fermi energy as filled, but no particle has a greater energy. This is entirely consistent with the Pauli exclusion principle where each quantum state can have one but only one particle.
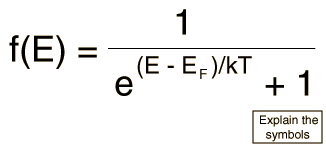
| Distribution functions | Numerical example |
| Fermi level in solids | Fermi level in band theory of solids |
Applied statistics concepts
| HyperPhysics***** Quantum Physics | R Nave |
