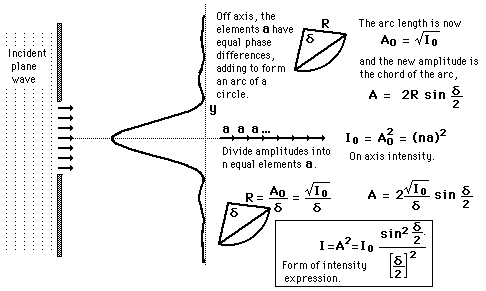
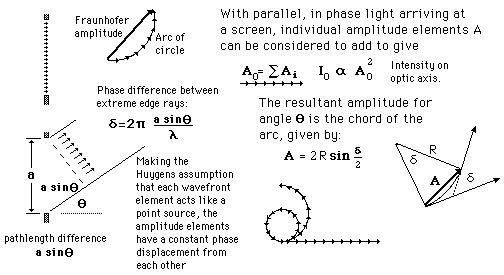
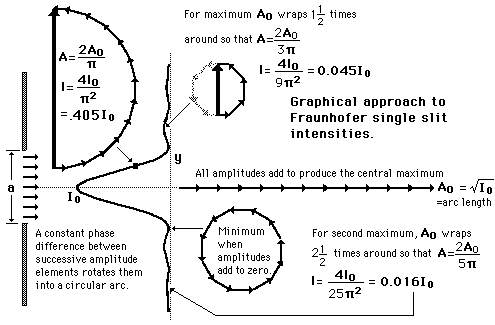
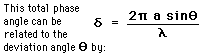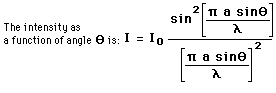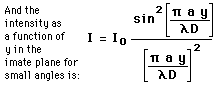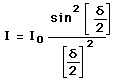Single Slit Diffraction Intensity
Under the Fraunhofer conditions, the wave arrives at the single slit as a plane wave. Divided into segments, each of which can be regarded as a point source, the amplitudes of the segments will have a constant phase displacement from each other, and will form segments of a circular arc when added as vectors. The resulting relative intensity will depend upon the total phase displacement 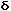 according to the relationship: according to the relationship:
|
Index
Diffraction concepts
Fraunhofer diffraction
Fraunhofer intensity concepts |
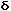 according to the relationship:
according to the relationship: