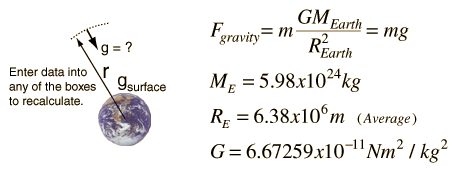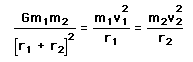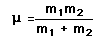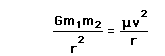Circular Orbit

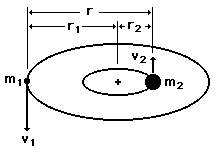
Gravity supplies the necessary centripetal force to hold a satellite in orbit about the earth. The circular orbit is a special case since orbits are generally ellipses, or hyperbolas in the case of objects which are merely deflected by the planet's gravity but not captured. Setting the gravity force from the univeral law of gravity equal to the required centripetal force yields the description of the orbit. The orbit can be expressed in terms of the acceleration of gravity at the orbit.

The force of gravity in keeping an object in circular motion is an example of centripetal force. Since it acts always perpendicular to the motion, gravity does not do work on the orbiting object if it is in a circular orbit.

Earth's Gravity

The weight of an object is given by W=mg, the force of gravity, which comes from the law of gravity at the surface of the Earth in the inverse square law form:

At standard sea level, the acceleration of gravity has the value g = 9.8 m/s², but that value diminishes according to the inverse square law at greater distances from the earth. The value of g at any given height, say the height of an orbit, can be calculated from the above expression.

Please note that the above calculation gives the correct value for the acceleration of gravity only for positive values of h, i.e., for points outside the Earth. If you drilled a hole through the center of the Earth, the acceleration of gravity would decrease with the radius on the way to the center of the Earth. If the Earth were of uniform density (which it is not!), the acceleration of gravity would decrease linearly to half the surface value of g at half the radius of the Earth and approach zero as you approached the center of the Earth.

Binary Circular Orbit

From the gravity force and the necessary centripetal force: If you are riding on one of the masses, the relative motion equation has the same form if you substitute the reduced mass which gives the orbit equation:

Reduced Mass