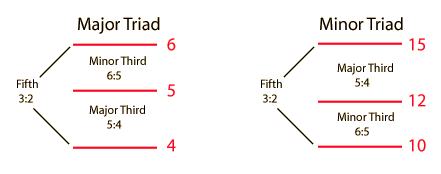
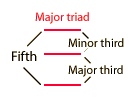
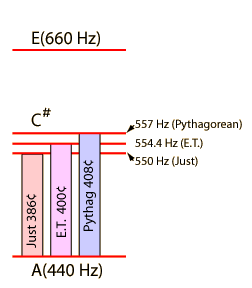
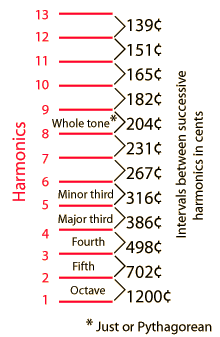
Harmonic Intervals in Cents

Expressing the musical intervals between successive harmonics in cents notation helps to show the relationship between the harmonics and the equal tempered musical scale. The equal tempered intervals are all in multiples of 100 cents, so the departure from such a multiple is an indication of how much the just interval is out of tune with equal temperament.

If any musical source produces a fundamental and a series of exact harmonices, then it is evident that the upper harmonics will be out of tune with the corresponding equal tempered notes. Examination of the illustration will make it evident that the 7th harmonic shows the most severe departure from any equal tempered interval. This is important in the design of brass instruments, since they use the upper resonances of the instrument as played notes in a harmonic sequence. Fortunately, the upper resonances of brass instruments can be tuned closer to equal temperament in the manufacturing process so that the problem is not so severe, but the seventh resonance is still troublesome.

Index

Temperament and musical scales
 
HyperPhysics***** Sound R Nave
 Go Back








Major and Minor Triads

The major and minor triads are used widely in western music. In terms of just musical intervals, these triads can be expressed as whole number ratios of frequencies. The actual frequencies vary slightly in other temperaments, but the labeling of the intervals is the same.

Note that the 4th, 5th and 6th harmonics of a harmonic sequence form a major triad: The pitch ratio 4:5:6 is the triad. The minor triad does not fit so neatly in the harmonic sequence, the smallest whole number ratios that produce a minor triad being 10:12:15.

Variation of major triad with temperament
 Index

Temperament and musical scales
 
HyperPhysics***** Sound R Nave
 Go Back





Major Triad Differences

The differences between Just, Pythagorean , and Equal Tempered scales becomes evident in the tuning of a triad. The fifth is essentially the same for the three temperaments, but the major third differences are significant.
The frequencies for the major triad A-C#-E are shown at left. The three different major thirds are labeled in cents, and the difference can be seen to be larger than the just noticeable difference of 5¢.

The difference between the Just and Phythagorean major thirds is 22¢, which is called the "syntonic comma". Nine commas make approximately a whole tone.

Pythagorean intervals
 Index

Temperament and musical scales

Reference
Rossing
Science of Sound, 2nd ed.
Ch 7
 
HyperPhysics***** Sound R Nave
 Go Back





Pitch Change with Temperature

Since the speed of sound in air is given approximately by

where TC is the celsius temperature,

then at temperature °C = °F,

the speed of sound is m/s = ft/s = mi/hr.

Since the pitch of air column instruments depend directly upon this speed of sound, then if the air column were at °C and were warmed by 1 °C, the pitch would increase (go sharp) by about cents.

If the column were warmed to °C, then it would be cents sharp.

Note that you don't have to know the actual frequencies for these calculations since musical intervals are defined as pitch ratios.

Pythagorean intervals
 Index

Temperament and musical scales

Reference
Rossing
Science of Sound, 2nd ed.
 
HyperPhysics***** Sound R Nave
 Go Back