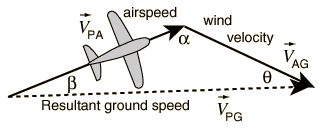
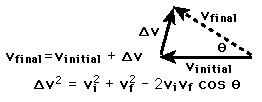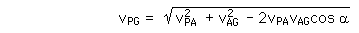Law of Cosines

The law of cosines for calculating one side of a triangle when the angle opposite and the other two sides are known. Can be used in conjunction with the law of sines to find all sides and angles.

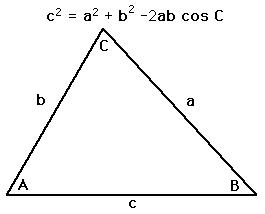Enter data for sides a and b and either side c or angle C. Then click on the active text for the unknown quantity you wish to calculate.
Calculation of side c is straightforward, but calculation of sides a or b is more involved since changing either side c or angle C forces changes in both a and b. To calculate a or b, first use the law of sines to find the angle opposite the side you wish to calculate. Then use the law of cosines to find the unknown side length.

Applications

Index

HyperPhysics*****HyperMath*****Trigonometry

R Nave

Go Back

Applications, Law of Cosines

The law of cosines has application to vector quantities:

To find the difference between two vectors, as in a glancing collision.

It has application along with the law of sines to the problem of the heading angle for an aircraft in the wind.

Other applications:

Lande' g-factor

Index

HyperPhysics*****HyperMath*****Geometry

R Nave

Go Back

Aircraft Heading to Counter Wind

Calculating the necessary aircraft heading to counter a wind velocity and proceed along a desired bearing to a destination is a classic problem in aircraft navigation. It makes good use of the law of sines and the law of cosines.

The angle q is just the difference between the wind direction and the desired bearing. With that angle and the law of sines, the offset angle b for the aircraft is obtained:

Then the law of cosines is applied to get the resultant ground speed:

Index

HyperPhysics*****HyperMath*****Geometry

R Nave

Go Back