Fundamental Forces
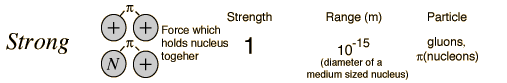

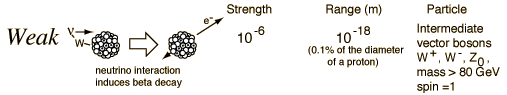
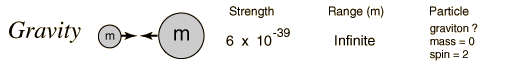
Fundamental force concepts
Coupling constants
| HyperPhysics***** Quantum Physics | R Nave |
Fundamental Forces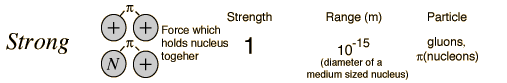  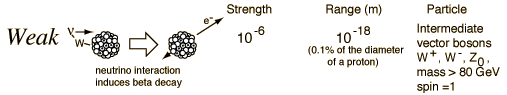 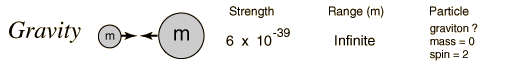 |
Index Fundamental force concepts Coupling constants | ||
|
Go Back |
The Strong Force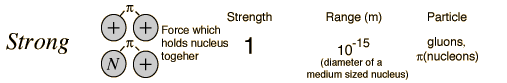 A force which can hold a nucleus together against the enormous forces of repulsion of the protons is strong indeed. However, it is not an inverse square force like the electromagnetic force and it has a very short range. Yukawa modeled the strong force as an exchange force in which the exchange particles are pions and other heavier particles. The range of a particle exchange force is limited by the uncertainty principle. It is the strongest of the four fundamental forces Since the protons and neutrons which make up the nucleus are themselves considered to be made up of quarks, and the quarks are considered to be held together by the color force, the strong force between nucleons may be considered to be a residual color force. In the standard model, therefore, the basic exchange particle is the gluon which mediates the forces between quarks. Since the individual gluons and quarks are contained within the proton or neutron, the masses attributed to them cannot be used in the range relationship to predict the range of the force. When something is viewed as emerging from a proton or neutron, then it must be at least a quark-antiquark pair, so it is then plausible that the pion as the lightest meson should serve as a predictor of the maximum range of the strong force between nucleons. 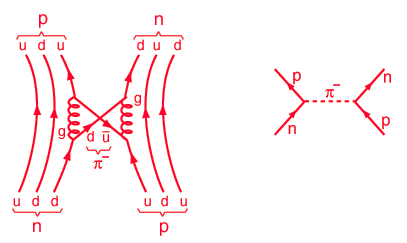 The sketch is an attempt to show one of many forms the gluon interaction between nucleons could take, this one involving up-antiup pair production and annililation and producing a π- bridging the nucleons.
|
Index Fundamental force concepts | ||
|
Go Back |
The Electromagnetic Force One of the four fundamental forces, the electromagnetic force manifests itself through the forces between charges (Coulomb's Law) and the magnetic force, both of which are summarized in the Lorentz force law. Fundamentally, both magnetic and electric forces are manifestations of an exchange force involving the exchange of photons . The quantum approach to the electromagnetic force is called quantum electrodynamics or QED. The electromagnetic force is a force of infinite range which obeys the inverse square law, and is of the same form as the gravity force. 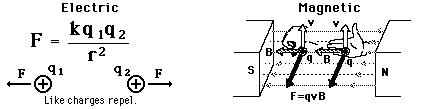 The electromagnetic force holds atoms and molecules together. In fact, the forces of electric attraction and repulsion of electric charges are so dominant over the other three fundamental forces that they can be considered to be negligible as determiners of atomic and molecular structure. Even magnetic effects are usually apparent only at high resolutions, and as small corrections. |
Index Fundamental force concepts | ||
|
Go Back |
The Weak Force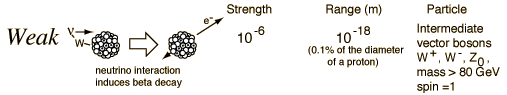 One of the four fundamental forces, the weak interaction involves the exchange of the intermediate vector bosons, the W and the Z. Since the mass of these particles is on the order of 80 GeV, the uncertainty principle dictates a range of about 10-18 meters which is about 0.1% of the diameter of a proton. The weak interaction changes one flavor of quark into another. It is crucial to the structure of the universe in that 1. The sun would not burn without it since the weak interaction causes the transmutation p -> n so that deuterium can form and deuterium fusion can take place. 2. It is necessary for the buildup of heavy nuclei. The role of the weak force in the transmutation of quarks makes it the interaction involved in many decays of nuclear particles which require a change of a quark from one flavor to another. It was in radioactive decay such as beta decay that the existence of the weak interaction was first revealed. The weak interaction is the only process in which a quark can change to another quark, or a lepton to another lepton - the so-called "flavor changes". The discovery of the W and Z particles in 1983 was hailed as a confirmation of the theories which connect the weak force to the electromagnetic force in electroweak unification. The weak interaction acts between both quarks and leptons, whereas the strong force does not act between leptons. "Leptons have no color, so they do not participate in the strong interactions; neutrinos have no charge, so they experience no electromagnetic forces; but all of them join in the weak interactions."(Griffiths)
|
Index Fundamental force concepts Reference Griffiths Ch 2 | ||
|
Go Back |
Feynman Diagrams for Weak Force
One of the four fundamental forces, the weak interaction involves the exchange of the intermediate vector bosons, the W and the Z. Since the mass of these particles is on the order of 80 GeV, the uncertainty principle dictates a range of about 10-18 meters which is about .1% of the diameter of a proton. The weak interaction changes one flavor of quark into another. For example, in the neutron decay depicted by the Feynman diagram at left above, one down quark is changed to an up quark, transforming the neutron into a proton. The primitive vertices in the Feynman diagrams for the weak interaction are of two types, charged and neutral. For leptons they take the following form 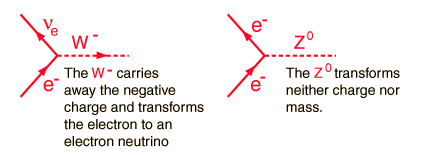 The electron is used as an example in these diagrams, but any lepton can be substituted on the incoming side. The exit side (top) will be the same for the neutral vertex, but determined by the charge of the W in the charged vertex. Besides conserving charge, the vertex must conserve lepton number, so the process with the electron can produce an electron neutrino but not a muon neutrino.
The charged vertices in the weak interaction with quarks take the form 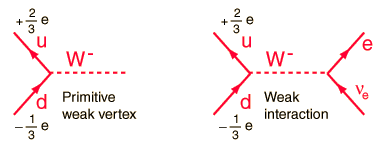 So it is seen that the quark changes its flavor when interacting via the W- or W+. As drawn, this interaction cannot be observed because it implies the isolation of an up quark. Because of quark confinement, isolated quarks are not observed. But rotating the Feynman diagram gives an alternative interaction, shown below for both electron and muon products. 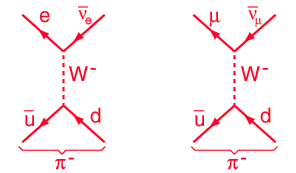 This suggests the weak interaction mechanism for the decay of the pion, which is observed to happen by the muon pathway. 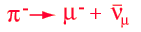 The weak interaction in the electron form at left above is responsible for the decay of the neutron and for beta decay in general.
|
Index Fundamental force concepts Reference Kaufmann Ch. 29 Griffiths Ch 2 | ||||||||||||
|
Go Back |