Motion with time dependent acceleration
Given an object which starts from position x=0 and moves along a straight line with position given by
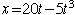
find:
a. The expression for velocity and the time at which the velocity is zero.
b. The expression for acceleration and the time at which the acceleration is zero.
c. The average velocity over the first 3 seconds of motion.
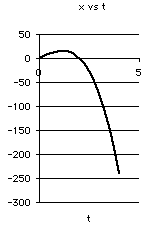
d. Show graphs of the position, velocity and acceleration for the first 4 seconds of motion.
Solution:
a. The velocity is given by the derivative of the position.
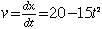 | and for v=0 the time is | 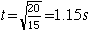 . . |
b. The acceleration is given by the derivative of the velocity.
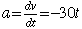 | and for a=0 the time is t=0. |
c. The average velocity must be calculated from the displacement divided by the time.
| (Caution! The expression | 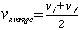 |
| is not valid for this case since the acceleration is not constant.) |
The average velocity for the first 3 seconds of motion is given by
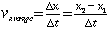 | where | 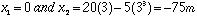 |
so the average velocity is -25 m/s. You can check to see that the constant acceleration expression for average velocity gives the erroneous value -22.5 m/s.
d. Motion graphs.
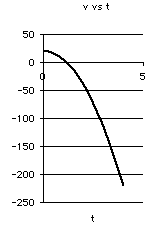
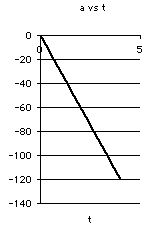
Motion equations as polynomials in time.
| Example problems in mechanics |
Polynomial derivatives