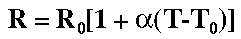Resistance: Temperature Coefficient

Since the electrical resistance of a conductor such as a copper wire is dependent upon collisional proccesses within the wire, the resistance could be expected to increase with temperature since there will be more collisions. An intuitive approach to temperature dependence leads one to expect a fractional change in resistance which is proportional to the temperature change:

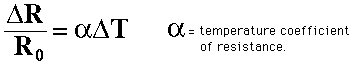
Or, expressed in terms of the resistance at some standard temperature from a reference table:

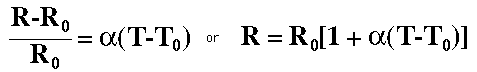
Low Temperature Resistivity

The temperature dependence of resistivity at temperatures around room temperature is characterized by a linear increase with temperature. Microscopic examination of the conductivity shows it to be proportional to the mean free path between collisions (d), and for temperatures above about 15 K, d is limited by thermal vibrations of the atoms. The general dependence is summarized in the proportionalities:

At extremely low temperatures, the mean free path is dominated by impurities or defects in the material and becomes almost constant with temperature. With sufficient purity, some metals exhibit a transition to a superconducting state.

Resistor Temperature Dependence

If a resistor of initial value

= ohms

at initial temperature

= C

is heated to temperature

= C

and has a temperature coefficient

= x 10^ / C

then the resistance will be

= ohms

Table of temperature coefficients