Gaussian Surfaces

Part of the power of Gauss' law in evaluating electric fields is that it applies to any surface. It is often convenient to construct an imaginary surface called a Gaussian surface to take advantage of the symmetry of the physical situation.

Conductor at Equilibrium

For a conductor at equilibrium:

1. The net electric charge of a conductor resides entirely on its surface. (The mutual repulsion of like charges from Coulomb's Law demands that the charges be as far apart as possible, hence on the surface of the conductor.)

2. The electric field inside the conductor is zero. (Any net electric field in the conductor would cause charge to move since it is abundant and mobile. This violates the condition of equilibrium: net force =0.)

3. The external electric field at the surface of the conductor is perpendicular to that surface. (If there were a field component parallel to the surface, it would cause mobile charge to move along the surface, in violation of the assumption of equilibrium.)

Electric Field: Conductor Surface

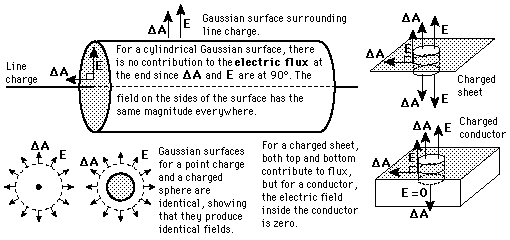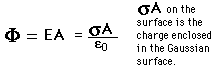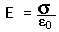
The fact that the conductor is at equilibrium is an important constraint in this problem. It tells us that the field is perpendicular to the surface, because otherwise it would exert a force parallel to the surface and produce charge motion. Likewise it tells us that the field in the interior of the conductor is zero, since otherwise charge would be moving and not at equilibrium.

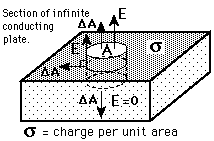
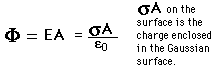
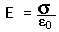
Examining the nature of the electric field near a conducting surface is an important application of Gauss' law. Considering a cylindrical Gaussian surface oriented perpendicular to the surface, it can be seen that the only contribution to the electric flux is through the top of the Gaussian surface. The flux is given by and the electric field is simply While strictly true only for an infinite conductor, it tells us the limiting value as we approach any conductor at equilibrium.