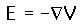Electric Field from Voltage
One of the values of calculating the scalar electric potential (voltage) is that the electric field can be calculated from it. The component of electric field in any direction is the negative of rate of change of the potential in that direction.
|
If the differential voltage change is calculated along a direction ds, then it is seen to be equal to the electric field component in that direction times the distance ds. 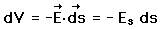 The electric field can then be expressed as
|
 |
For rectangular coordinates, the components of the electric field are
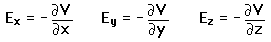
|
|
Voltage concepts
Electric field concepts
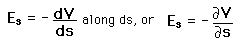
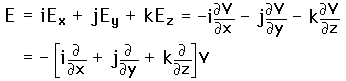
 . The electric field can then be written
. The electric field can then be written