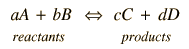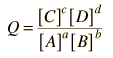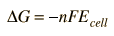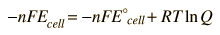Standard Electrode Potentials

In an electrochemical cell, an electric potential is created between two dissimilar metals. This potential is a measure of the energy per unit charge which is available from the oxidation/reduction reactions to drive the reaction. It is customary to visualize the cell reaction in terms of two half-reactions, an oxidation half-reaction and a reduction half-reaction.

The cell potential (often called the electromotive force or emf) has a contribution from the anode which is a measure of its ability to lose electrons - it will be called its "oxidation potential". The cathode has a contribution based on its ability to gain electeons, its "reduction potential". The cell potential can then be written

If we could tabulate the oxidation and reduction potentials of all available electrodes, then we could predict the cell potentials of voltaic cells created from any pair of electrodes. Actually, tabulating one or the other is sufficient, since the oxidation potential of a half-reaction is the negative of the reduction potential for the reverse of that reaction. Two main hurdles must be overcome to establish such a tabulation

1. The electrode potential cannot be determined in isolation, but in a reaction with some other electrode.
2. The electrode potential depends upon the concentrations of the substances, the temperature, and the pressure in the case of a gas electrode.

In practice, the first of these hurdles is overcome by measuring the potentials with respect to a standard hydrogen electrode. It is the nature of electric potential that the zero of potential is arbitrary; it is the difference in potential which has practical consequence. Tabulating all electrode potentials with respect to the same standard electrode provides a practical working framework for a wide range of calculations and predictions. The standard hydrogen electrode is assigned a potential of zero volts.

The second hurdle is overcome by choosing standard thermodynamic conditions for the measurement of the potentials. The standard electrode potentials are customarily determined at solute concentrations of 1 Molar, gas pressures of 1 atmosphere, and a standard temperature which is usually 25°C. The standard cell potential is denoted by a degree sign as a superscript.

The example below shows some of the extreme values for standard cell potentials.

The values for the table entries are reduction potentials, so lithium at the top of the list has the most negative number, indicating that it is the strongest reducing agent. The strongest oxidizing agent is fluorine with the largest positive number for standard electrode potential. The link below takes you to a more extensive table.

Useful applications of the standard electrode potentials include the following.

Calculation of Voltaic Cell Potentials

When an electrochemical cell is arranged with the two half-reactions separated but connected by an electrically conducting path, a voltaic cell is created. The maximum voltage which can be produced between the poles of the cell is determined by the standard electrode potentials under the standard conditions under which those potentials are defined.

Consider the historic Daniell cell in which zinc and copper were used as electrodes. The data from the table of standard electrode potentials is

The cell potential can be written

Since the tabulated standard electrode potentials are reduction potentials, the one which is most negative will need to be reversed in sign to get its oxidation potential. When that is done, it is clear that the theoretical standard cell potential for the zinc-copper cell is 1.10 volts.

In general, a real voltaic cell will differ from the standard conditions, so we need to be able to adjust the calculated cell potential to account for the differences. This can be done with the application of the Nernst equation.

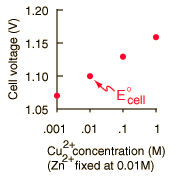
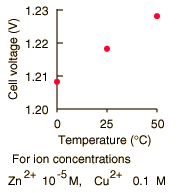
By numerically exploring the above calculation, you can confirm that large concentration differences between the anions and the cations can cause the voltage to differ significantly from the standard cell potential, and that such large concentration differences also make the cell potential more temperature dependent.

The Nernst Equation

The cell potential for a voltaic cell under standard conditions can be calculated from the standard electrode potentials. But real voltaic cells will typically differ from the standard conditions. The Nernst equation relates the cell potential to its standard cell potential.

R = gas constant T = temperature in Kelvins Q = thermodynamic reaction quotient F = Faraday's constant n = number of electrons transferred

The quantity Q, the thermodynamic reaction constant, is like a dynamic version of the equilibrium constant in which the concentrations and gas pressures are the instantaneous values in the reaction mixture. For a reaction

the reaction quotient has the form

where [C] is understood to be the molar concentration of product C, or the partial pressure in atmospheres if it is a gas.

Applied to the Daniell cell where zinc and copper form the electrodes, the reaction is

the form of Q is

since the concentrations of the pure metal solids are assigned the value 1. This implies that the departure of the cell potential from its standard value of 1.10 volts will be influenced by the temperature and the ion concentrations.

One implication is that the cell potential will be reduced from the standard value if the concentration of Zn2+(aq) is greater than that of Cu2+(aq) at the standard temperature. An excess concentration of Cu2+(aq) will give a higher voltage. The graph at right shows the increase in cell voltage with increasing concentration of the cation. Note that the horizontal axis is logarithmic, and that the straight line variation of the voltage represents an logarithmic variation with Q. Note that the cell potential is equal to the standard value if the concentrations are equal even if they are not equal to the standard value of 1M, since the logarithm gives the value zero.

Consider a concentration of 10-5Molar for Zn2+(aq) and 0.1 Molar for Cu2+(aq) as a test case for temperature dependance. We can see that the cell potential tends to increase with temperature, or that a colder cell prodices less voltage - a commonly observed phenomenon with dry cell batteries. The variation with temperature is linear with temperature, but quite small for this cell. The large variations of practical output voltage with temperature for dry cells does not arise from the Nernst equation alone.

Background for the Nernst Equation

The Nernst equation allows us to predict the cell potential for voltaic cells under conditions other than standard conditions of 1M, 1 atmosphere, 25°C. The effects of different temperatures and concentrations may be tracked in terms of the Gibbs free energy change DG. This free energy change depends upon the temperature and concentrations according to

where DG^° is the free energy change under standard conditions and Q is the thermodynamic reaction quotient. The free energy change is related to the cell potential E_cell by

or

which is called the Nernst equation.